Algorithmes de Résolution des SUDOKUS
Algorithme stochastique
Principe
L'algorithme stochastique est un outil d'optimisation très puissant, utilisé pour faire face à des problèmes difficiles utilisant des techniques de simulation numériques de chaînes de Markov. Il est utilisé dans de nombreux algorithmes génétiques: -> Algorithme de génétique culturelle : -> Optimisation par essain de particule : Cet algorithme reproduit des processus d'évolution ou d'apprentissage selon des règles physiques ou issues de l'évolution naturelle. Il repose sur des processus aléatoires.
Appliqué au Sudoku
Le principe est simple, l'algorithme remplit toutes les cases de la grille vide. Il calcule ensuite sur chaque ligne et chaque colonne le nombre de doublons et les conserves dans un tableau. Il se spécifie ensuite à la zone oú il y a le plus de doublons puis tente de nouveaux mélanges aléatoires jusqu'à ce que le nombre d'erreurs ne soit plus le maximum et ensuite il se spécifie à la nouvelle zone oú il y a le plus de doublons. Il s'arrête lorsque plus aucune case ni colonne n'a de doublons.
Malgrès le fait que cet algorithme puisse résoudre les grilles de sudoku ce n'est pas le plus adaptés à ce type de problème vu le grand nombres d'opérations effectuées en trop à cause de l'aléatoire qui ne vérifie pas la condition pour chaque cellule avant de la remplir.
Résolution du Sudoku
Voici un exemple de l'application de l'algorihtme détaillé ci-dessus:
La grille est remplie une première fois aléatoirement sans verifier que la condition ne soit respectée. On identifie ensuite pour chaque ligne et chaque colonne le nombre de doublons. Pour la ligne 1, il y a deux 2 et deux 3 ce qui fait deux doublons. Pour la colonne 1, il y a juste deux 8, il y a donc un doublon. On repère la zone oú il y a le plus de doublons afin de tenter de l'améliorer à la prochaine étape.
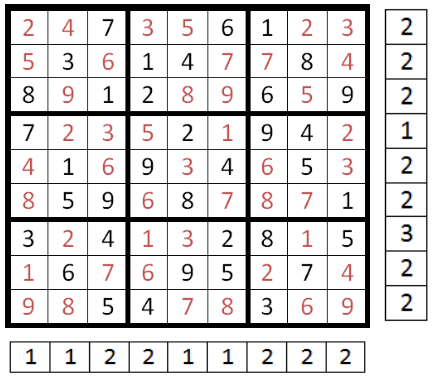
Le bloc en bas à droite contient le plus grand nombre d'erreur, on modifie aléatoirement les nombres du bloc et on recalcule le nombre d'erreur. Il a diminué sur certaines lignes et a augmenté sur d'autres.
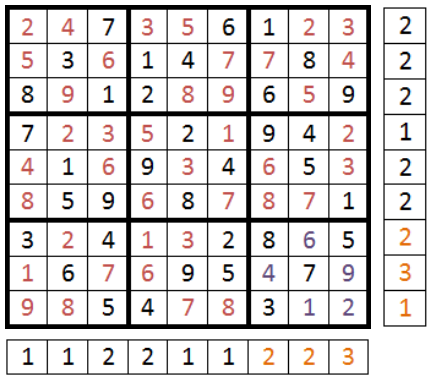
On remodifie le bloc aléatoirement et on modifie également celui du dessus. On recalcule les doubons et on constate le résultat. Le nombre de doublons a diminué par rapport à la grille précédente.
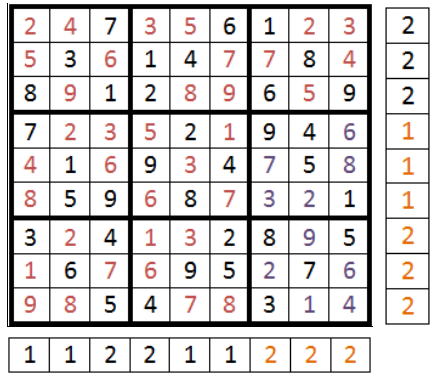
On effectue le mélange à présent sur le bloc en haut à droite puisqu'il fait partie de ceux ayant le plus de doublons. On recalcule le nombre de doublons et l'on s'aperçoit que l'on a réussi à faire diminuer les colonnes 7 et 8 d'un doublons.
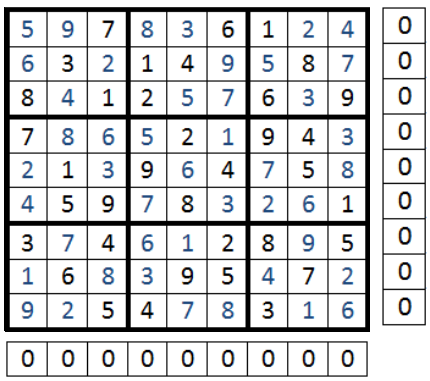
On réalise ces opérations jusqu'à ce que l'on ai plus aucun doublons dans la grille, le solution sera alors trouvée.
