Algorithmes de Résolution des SUDOKUS
Backtracking
Principe
Le backtracking est une forme de parcours en profondeur d'un arbre avec des contraintes sur les noeuds
L'idée est de partir du noeud parent, descendre dans le premier noeud fils satisfaisant la contrainte. Ce noeud fils devient alors un noeud parent et l'on parcourt ensuite ses noeuds fils sous le même principe.Lorsque l'on a parcouru tous les noeuds fils d'un noeud et qu'aucun ne satisfait la contrainte, on remonte alors au noeud parent et on descend dans le noeud fils suivant. Si l'on arrive au dernier fils du premier noeud parent et qu'il ne satisfait pas la contrainte alors il n'existe pas de solution. La solution est identifiée lorsque l'on arrive à un noeud qui satisfait la contrainte et qui n'a pas de noeud fils.
Fonctionnement
Afin de minimiser la complexité de l'algorithme du backtracking appliqué au Sudoku il faut eviter au maximum le nombre de possibilités. Plus le nombre de possibilités est important plus les risques d'erreur et retour en arriére tardif(remonté aux noeuds parents) sont nombreux. Afin de minimiser le risque d'erreur et donc le nombre d'opérations réalisées, il faut déterminer un ordre de parcour de la grille, en remplissant les cases ayant le moins de possibilités de nombre aux cases en ayant le plus. Pour effectuer se parcours l'algorithme utilise une liste chaînée qui s'occupera de la mémorisation de l'ordre de remplissage de la grille.
La vérification des possibilités se fera à l'aide de variable globale qui auront pour but de mémoriser les valeurs déjà renseignées dans la grille afin de limiter les opérations de parcours
L'algorithme
On classe les cases de celles ayant le moins de possibilités à celles en ayant le plus. On place ce classement dans une liste. On parcours la liste jusqu'à arriver à la derniere cellule de la liste. Pour chaque cellule de la liste: - On teste les valeurs de 1 à n²: - si la valeur est possible : - on l'inscrit dans la cellule et on passe à la suivante - sinon : - on remontre à la cellule suivante et on reprend le test des valeurs de 1 à n² à partir de la valeur déjà inscrite dans la cellule.
Code de la fonction récursive:
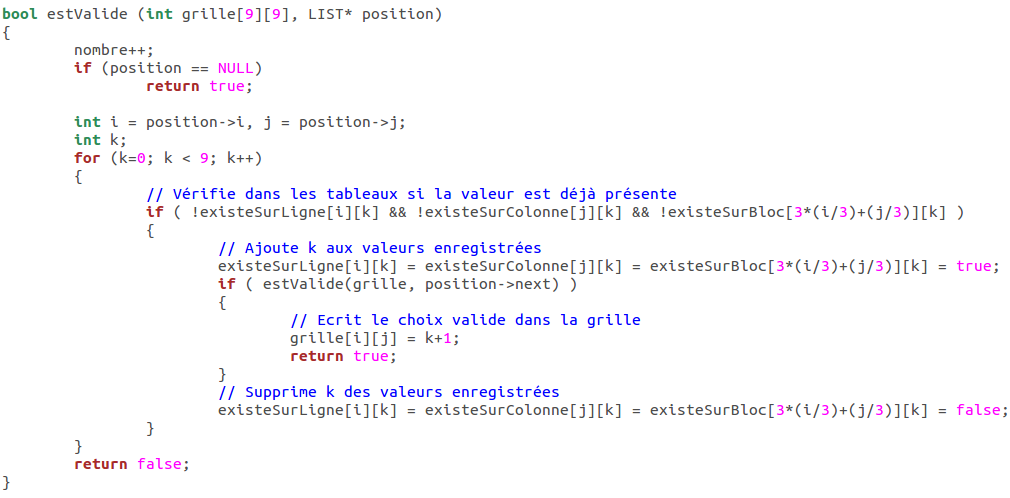
Résolution du Sudoku
Voici un exemple de résolution d'une grille de Sudoku (n=3) avec l'algorithme du backtracking énoncé ci-dessus.
Dans un premier temps on détermine l'ordre de remplissage des cellules pour chaque case de la grille. (Illustration ci-dessous)
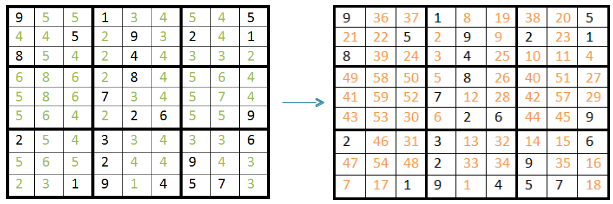
On part de la cellule n°1, on teste les valeurs possibles de 1 à 9. Le premier chiffre possible est 6, on place 6 dans la case et on passe à la suivante.
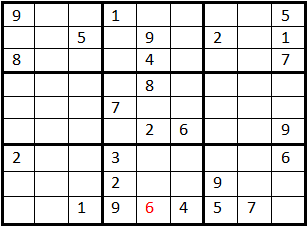
On arrive à la cellule suivante, la 2 et de la même façon on teste les valeurs de 1 à 9 et on place la première possible.
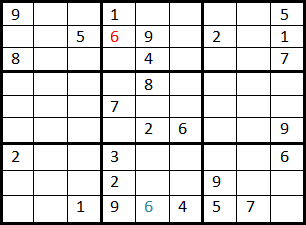
On effectue ce parcourt jusqu'à arriver à la première situation bloquante, la cellule n°23. Dans cette case aucune valeur de 1 à 9 n'est possible, on remonte donc à la cellule 22, oú il y a un 3, on reprend alors le test des valeurs pour cette case de 3 à 9.
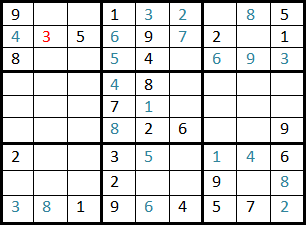
De la même façon que pour la cellule 23, la cellule 22 devient une situation bloquante donc on remonte à la cellule 21 et on effectue le même procédé jusqu'a ce que l'on arrive à avoir une solution.
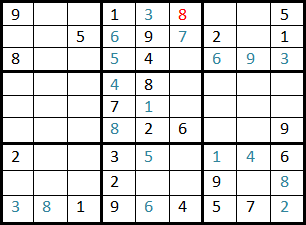
On effectue ces operations jusqu'à ce que l'on soit arrivé à remplir la dernière case de la grille.