Algorithmes de Résolution des SUDOKUS
Couverture Exacte
Principe
Définition
Voici la définition mathématique de la couverture exacte fournie par Wikipédia: Etant donné un univers U d'éléments et une collection S d'ensemble, une couverture exacte est un sous-ensemble S* de S tel que tout élements de U est aussi un element dans exactement un des ensembles de S*. En d'autres termes, une couverture exacte est une sous-collection S* de S qui est une partition de U : les ensemble dans S* son disjoints et leur union est U.
Explication par l'exemple
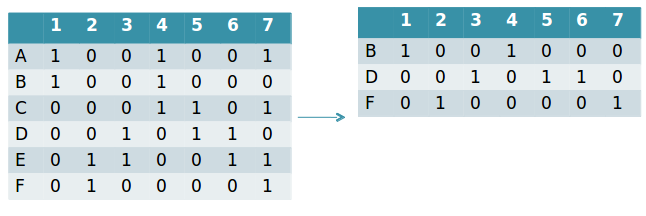
Soit l'univers U = { 1, 2, 3, 4, 5, 6, 7} et S { A, B, C, D, E, F } tel que : A = { 1, 4, 7}, B = { 1, 4}, C = { 4, 5, 7} , D = { 3, 5, 6} , E = { 2, 3, 6, 7} , F = { 2, 7} alors S* = {B,D,F} En selectionnant les ensembles B, D, F, nous obtenons une fois et juste une seule fois tout les éléments de U.
On peut observer ce problème sous forme de représentation matricielle également.
Dancing Links
L'algorithme X permet de solutionner ce problème de couverture exacte, il s'agit d'un algorithme de recherche récursif utilisant le principe du backtracking : le retour sur trace. Les dancing links sont une méthode d'implémentation de cet algorithme X, ils utilisent des listes doublement chaînées.
Voici une représentation d'une matrice à l'aide des dancing links
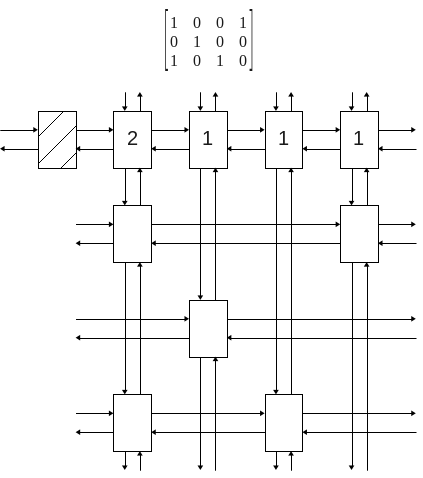
Résolution du Sudoku
Pour permettre l'application de cet algorithme sur une grille de sudoku, il faut réaliser sa matrice. La matrice est réalisée selon quatres contraintes : -> Chaque cellule doit contenir exactement un nombre; -> Chaque ligne doit contenir chacun des n² nombres exactement une seule fois. -> Chaque colonne doit contenir chacun des n² nombres exactement une seule fois. -> Chaque bloc doit contenir chacun des n² nombres exactement une seule fois.
Voici un exemple de matrice de couverture exacte utilisée pour résoudre une grille de Sudoku n=2.Matrice