Programmation dynamique

Utilisation concrète

Le Seam Carving

Le seam carving (ou recadrage intelligent), est un algorithme de redimensionnement d'image développé par Shai AVIDAN et Ariel SHAMIR. Cet algorithme redimensionne, non pas par une mise à l'échelle ou un recadrage classique, mais par une suppression des pixels dits "de moindre importance".

L'importance d'un pixel est en général mesurée par son contraste comparé à ses plus proches voisins (on parle plus précisément de leur énergie, mais aborder cette notion sortirait du contexte), mais d'autres techniques, comme de détections de formes, peuvent-être utilisées.

De plus, il est possible de définir, ou de détecter automatiquement, des zones de grandes importances et ainsi de les protéger de toutes suppressions. À l'inverse, on peut définir des zones pouvant être retirées en priorité. De ces informations, l'algorithme détecte les chemins de plus basse énergie (les moins indispensbles, ceux qui portent le moins d'information utile) et les supprime.

Explication par l'exemple

Afin de présenter cette technique, nous allons travailler avec une image d'exemple et nous allons comparer les résultats obtenus via un traitement standard avec ceux que le seam carving nous permettent d'obtenir. Partons de de l’image suivante, que l’on souhaite faire tenir dans un carré :


Image originale

Les deux traitement typiques que l’on pourrait appliquer sont :


À gauche : image rognée - à droite : image redimensionnée

Le résultat que nous aurions en utilisant le seam carving serait le suivant : l'image serait redimensionnée intelligemment aux proportions souhaitées, en conservant les aspects des différents objets qui semblent être les principaux sujets représentés. Voici donc ci-dessous l'illustration de l'application de la technique du seam carving pour répondre à notre problématique :


À gauche : image originale - à droite : image redimensionnée intelligemment

En comparant l’image originale et celle obtenue après traitement, on constate que les éléments qui la composent ont gardé leur aspect, leurs proportions, mais on été rapprochés : c’est basiquement ce que propose le seam carving.

Ainsi, nous avons pu aborder ce que cette méthode fait ; voyons à présent comment cela fonctionne et quel est concrètement l'apport de la programmation dynamique dans la mise en place de cette fonctionnalité.

Comment ça marche

Nous nous intéressons à l'application des méthodes de programmation dynamique dans la résolution d'un problème. Ainsi, il va nous falloir ici comprendre comment est mis en place cette manipulation qu'est le seam carving.

Comme nous l'avons évoqué précédemment, le premier traitement à effectuer sur l'image à redimensionner est le calcul du poids (on parle aussi parfois de densité ou d'énergie) de chaque pixel de l'image, afin d'obtenir une carte des zones de haute énergie, comme illustré sur les figures suivantes :


À gauche : image originale - à droite : carte des zones de haute énergie

Dans la figure à droite, ci-dessus, plus une zone est dense, plus elle est blanche. Ainsi les zones de densité très faibles sont noires et ne sont pas intéressantes du point de vu du contenu de notre image : elles ne représentent pas de sujet avec un aspect ou des proportions particulières ; on pourrait les écraser ou les étirer sans que cela ne soit perturbant. On remarque donc que les les zones de haute densité sont essentiellement agglomérées au niveau du chateau et du personnage, mais également au niveau de certains motifs que l'on retrouve dans les nuages.

Dans cette présentation, nous ne nous intéresserons pas à l'algorithme utilisé pour déterminer ces zones, d'autant plus que de nombreuses solutions sont possibles et que celles-ci donnent des résultats très différents, plus ou moins adaptés selon le contenu de l'image et le traitement que l'on souhaite lui appliquer.

Problème de la somme de chemin maximale

À présent, pour diminuer la largeur de l’image, nous allons chercher à déterminer des chemins verticaux qui traversent le moins de zones d’énergie, pour ciseler l’image en retirant une à une chaque jointure (chaque seam) de moindre importance : l’idée de cet algorithme est qu’à chaque seam soustrait, l’image est moins large d’un pixel.

Comme on s'en doute, parcourir chaque combinaison de pixels de l’image pouvant former un chemin vertical serait un algorithme beaucoup trop lourd à utiliser : prenons l’exemple du fameux problème de la somme de chemin maximale. Il s'agit d'un problème typique dont la résolution la plus efficace utilise la programmation dynamique. Il consiste en l'exercice suivant :

En commençant en haut du triangle suivant et en additionnant à chaque étape l’un des nombres adjacents de la ligne en-dessous, trouvez la somme maximale que l’on peut obtenir en parcourant le triangle de son sommet jusqu'à sa base.

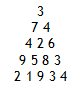
Dans ce triangle, la somme de chemin maximale est 29, on l'obtient en faisant 3 + 7 + 2 + 8 + 9, comme illustré en rouge ci-dessous :


À gauche : le triangle initial - à droite : le chemin solution

Il est important de constater qu’il ne s’agit pas systématiquement de choisir le nombre adjacent suivant le plus grand : par exemple, après le 7, on constate qu’un chemin passant par 2 aura un poids plus grand que tous ceux qu’on peut obtenir en passant par 4 : nous avons donc 2hauteur-1 chemins possibles pour parcourir le triangle.

Avec nos images, ce ne sont pas seulement deux, mais bien trois directions qui sont envisageables à chaque ligne (le pixel à la diagonale gauche, celui à la diagonale droite et celui immédiatement en-dessous). De plus, notre espace de travail n’a pas qu’un unique sommet, mais peut-être plusieurs milliers (autant de sommets que la largeur de l’image originale). Ainsi, pour une image de largeur w et de hauteur h, le nombre de chemins possibles est de w*3h : un parcours naïf de toutes ces combinaisons serait de complexité algorithmique exponentielle, donc inutilisable.

Application de la programmation dynamique

À présent, nous allons voir comment utiliser la programmation dynamique pour résoudre ce problème de détermination des seams de moindre importance.

Considérons notre carte des zones de haute énergie comme étant un tableau de pixels. Nous allons utiliser la représentation ci-dessous pour dérouler notre algorithme de programmation dynamique :


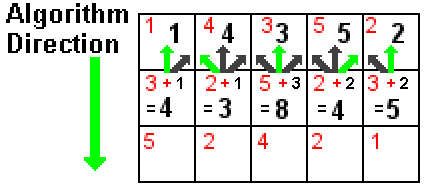
L'abstraction de notre image pour le déroulement de l'algorithme

Chaque case du tableau représente un pixel de l’image :

Les pixels de la première ligne ne peuvent pas avoir de provenance antérieure, puisqu'ils sont au sommet de l'image : ainsi leur somme cumulative (en noir) est simplement la valeur de leur énergie (en rouge).

Pour la deuxième ligne, considérons par exemple le second pixel : son énergie est 2 (en rouge). En regardant au niveau de la ligne précédente, nous avons le choix entre trois provenances :

Puisque 1 est la plus petite des ces trois valeurs, l'algorithme ignore les deux chemins et nous pouvons ainsi déterminer que la somme cumulative des énergies des pixels "traversés" pour arriver jusqu'à celui-ci est de poids 2 (son énergie) + 1 (la somme du chemin de provenance minimale), soit 3 (en noir).

Il s'agit ensuite simplement de répéter l'opération pour chaque pixel de chaque ligne jusqu'à avoir rempli notre image, pour finalement obtenir le tableau suivant :


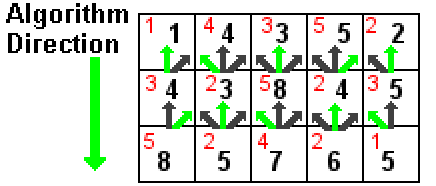
Détermination des sommes cumulatives pour l'ensemble des pixels de l'image

À présent, en partant du bas de l’image, nous pouvons voir apparaître les seams de moindre énergie : ce sont les chemins que nous pouvons parcourir en suivant les flèches vertes depuis les pixels dont la somme cumulative (valeur en noir dans la dernière ligne) est la plus faible. L'illustration suivante nous permet de détecter deux chemins de valeur minimum :


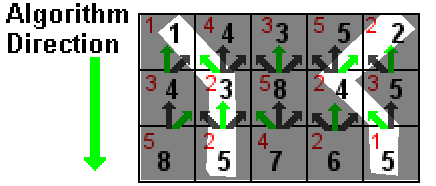
Les chemins de sommes minimales dans notre image

Ainsi, notre algorithme est à présent de complexité algorithmique linéaire.

Comment ça marche (suite)

Ainsi nous avons déterminé, en utilisant la programmation dynamique, les "colonnes" de pixels qui ont le moins d’énergie, ceux que l’on peut supprimer (ou dupliquer, selon que l’on souhaite rétrécir ou élargir l’image) en priorité.

Dans l'illustration ci-dessous, nous avons superposé les seams à la carte des zones de haute densité correspondant à l'image sur laquelle nous travaillons : plus ceux-ci sont d’un rouge vif, plus leur densité est faible et donc leur priorité élevée.


À gauche : carte des zones de haute énergie - à droite : mise en surbrillance des seams prioritaires

Enfin, nous n'avons plus qu'à supprimer autant de ces chemins qu'il nous est nécessaire pour réduire notre image d'autant que nous le souhaitons. Voici le résultat que nous obtenons :


De gauche à droite : image originale, mise en surbrillance des seams prioritaires, image traitée


De gauche à droite : zones de haute énergie, mise en surbrillance des seams prioritaires, zones de haute énergie redimensionnée

En comparant l’image originale et celle obtenue après traitement, on constate que les éléments qui composent cette dernière ont gardé leur aspect et leurs proportions, mais on été rapprochés : il s'agit du traitement réalisé basiquement par le seam carving, mais de bien plus nombreuses possibilités sont présentées par Shai AVIDAN et Ariel SHAMIR ; je vous recommande cette présentation (vidéo embarquée ci-dessous) si vous vous intéressez à leur travail concernant cette technique.