Programmation dynamique
L'approche ascendante
Modèle de référence : l'approche récursive
Afin d'aborder l'approche dite "de bas en haut" sur laquelle la programmation dynamique est élaborée, commençons par approfondir un peu notre étude des méthodes de type diviser & régner. Les algorithmes de ce type appliquent généralement l'une ou l'autre de ces deux stratégies :
- la récursivité sur les données : séparation des données en (au moins) deux parties quelconques, puis résolution des sous-problèmes (par la même fonction), puis enfin combinaison des résultats (e.g. : tri fusion).
- la récursivité sur le résultat : pré-traitement pour découpage des données puis résolution des sous-problèmes de manière à ce que les sous-résultats se combinent d'eux-mêmes à la fin (e.g. : tri rapide).
Ainsi, la méthode divide & conquer, bien que pouvant proposer deux stratégies, ne fournit qu'une seule approche : la récursivité.
La récursivité est une approche dite "de haut en bas" (ou descendante) : c'est-à-dire que les sous-problèmes sont résolus lorsqu'un problème parent est suffisamment complexe pour nécessiter leur résolution.
Comparaison des approches ascendantes et descendantes
Comme nous l'avons déjà déclaré, l'approche de résolution des problèmes à l'aide des méthodes de programmation dynamique est dite ascendante ou allant "de bas en haut" : il s'agit du sens contraire à celui utilisé par les méthodes récursives.
Afin d'illustrer les différences entre ces deux méthodes, nous nous appuyerons sur le schéma suivant :
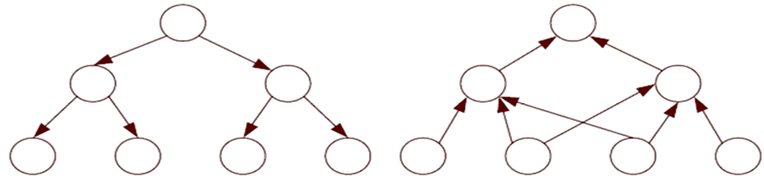
À gauche : diviser & régner - à droite : programmation dynamique
Dans cette figure, le problème à résoudre est représenté par la racine de l'arbre, et les descendants sont les sous-problèmes, plus faciles à résoudre. Dans la programmation dynamique, les feuilles constituent souvent les données de l’algorithme.
La principale différence entre ces deux méthodes est que la méthode diviser & régner est récursive (les calculs se font de haut en bas), tandis que la programmation dynamique est une méthode dont les calculs se font de bas en haut : on commence par résoudre les plus petits sous-problèmes et c’est en combinant leurs solutions que l’on résout des problèmes de plus en plus grands.
Apports de l'approche ascendante
Cette différence dans l'organisation de la résolution des sous-problèmes induit en fait des effets non négligeables, qui apparaissent également sur cette figure : la programmation dynamique permet aux sous-problèmes de se superposer. En effet, comme illustré sur la figure précédente, les sous-problèmes, dans la programmation dynamique, peuvent être en interaction, alors qu'avec les méthodes de type diviser & régner, ils ne le sont pas.
Autrement dit, là où l’approche diviser & régner crée des sous-problèmes absolument séparés et pouvant être résolus indépendamment les uns des autres, la programmation dynamique nous permet d'utiliser un même sous-problème dans la solution de plusieurs problèmes plus complexes : cela représente en réalité une fabuleuse optimisation algorithmique.