Mathématiques pour l'informatique 4 (option L3)¶
Ce cours abordera deux chapitres totalement indépendants du corpus standard des mathématiques pour informaticiens :
Résolution de récurrences, méthode des séries génératrices (5 séances)
Arithmétique élémentaire (4 séances)
On peut se faire une idée d'ensemble du domaine en consultant le livre Mathématiques Concrètes, qui reprend essentiellement le cours de Donald Knuth à Stanford. Le présent cours correspondrait à peu près aux chapitres 4 et 7 de ce livre.
L'étude des récurrences est indispensable pour l'analyse des algorithmes. La plupart des algorithmes intéressants sont décrits de manière récursive : on ramène la résolution d'un problème sur $n$ données (par exemple, trier une liste de $n$ éléments) à la résolution d'un ou plusieurs problèmes de taille inférieure. Si le temps de calcul est donné par une fonction $f(n)$, alors $f(n)$ peut se calculer à partir de la connaissance de $f(n-1), f(n-2),...$ etc. Ces techniques sont décrites dans ce livre.
L'arithmétique est l'étude des nombres entiers. C'est un vaste sujet dont on n'abordera que quelques aspects, en particulier l'arithmétique modulaire, indispensable à la compréhension de la cryptographie moderne et de nombreux autres aspects des communications numériques (codes correcteurs, compression, traitement du signal ...).
Chaque cours sera suivi d'une séance de TD sur machine. On utilisera le langage Python et son module de calcul formel sympy, dans l'environnement jupyter. Les comptes rendus de TD seront à renvoyer chaque semaine (par email à jyt@u-pem.fr) avant le début du cours suivant.
Récurrences et algorithmes récursifs¶
Introduction : les tours de Hanoï¶
Il est traditionnel d'introduire la notion de récursivité sur l'exemple du jeu des tours de Hanoï. Rappelons que le jeu se présente sous forme d'une planche munie de 3 tiges. Sur la tige 1 sont empilés 8 disques de diamètres décroissants. Le problème consiste à transférer les 8 disques sur la tige 3, en respectant les deux règles :
On déplace un seul disque à la fois
on ne doit pas poser un disque sur un disque plus petit
Pour inciter le lecteur à réfléchir, la description du jeu est accompagnée d'une fausse légende, mentionnant 64 disques d'or sur des aiguilles de diamant : "Nuit et jour, les prêtres se succèdent sur les marches de l’autel, occupés à transporter la tour de la première aiguille de diamant sur la troisième, sans s’écarter des règles fixes que nous venons d’indiquer, et qui ont été imposées par Brahma. Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes !". Connaissant le temps nécéssaire au déplacement d'un disque, pouvons-nous calculer la date de la fin du monde ? Pour cela, il nous faut résoudre d'une manière générale le problème à $n$ disques.
Soit donc $T(n)$ le nombre de mouvements nécéssaires pour déplacer une pile de $n$ disques d'une tige à une autre. Si $n=0$, $T(0)=0$. Si $n=1$, $T(1)=1$. Si $n=2$, on déplace le petit disque de 1 à 2 (notation $1\rightarrow 2$), le grand de 1 à 3 ($1\rightarrow 3$) puis le petit de 2 à 3 ($2\rightarrow 3$). Il faut donc 3 mouvements. Avec $n=3$, on transfère les deux disques du haut sur la tige 2 (B) au moyen de 3 mouvements, le grand disque de 1 (A) à 3 (C) en un mouvement, puis de nouveau les deux petits disques de 2 (B) à 3 (C). Au total, $T(3) = T(2)+1+T(2)=3+1+3 = 7$.
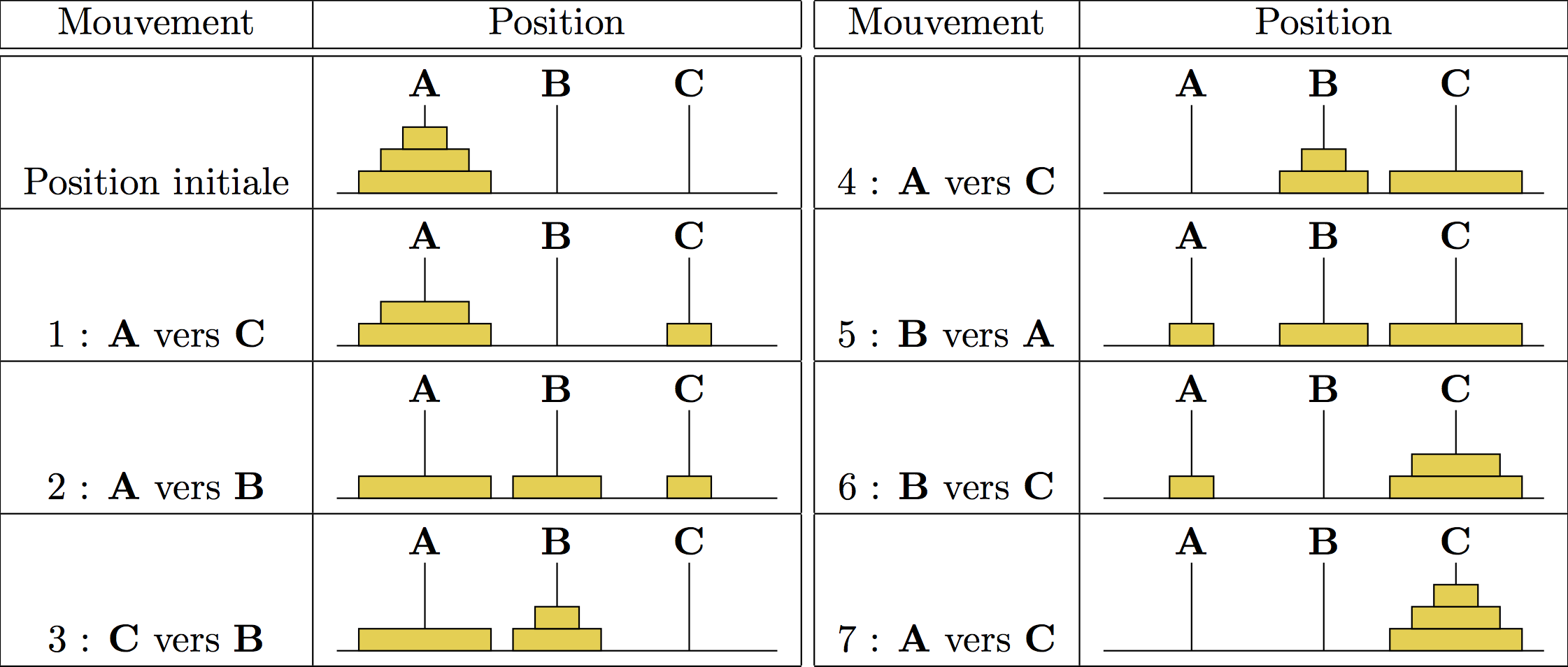
La structure récursive apparait clairement. Pour déplacer $n$ disques de 1 à 3, il faut libérer le grand disque $n$ en plaçant les autres sur la tige 2 ($T(n-1)$ mouvements), le déplacer de 1 à 3 (un mouvement), puis replacer les autres par dessus (encore $T(n-1)$ mouvements). On a donc la récurrence $$T(n) = 2T(n-1)+1$$ avec la condition initiale $T(0)=0$.
Ceci permet de calculer facilement les valeurs suivantes de $T(n)$ :
def T(n):
if n==0: return 0
return 2*T(n-1)+1
[T(n) for n in range(12)] # pas besoin de "print" en mode interprété
T(64) # Pour calculer la date de la fin du monde
T(64)/(3600*24*365*10**9) # Temps de résolution, en milliards d'années, en supposant un mouvement par seconde
Méthode 1 : la divination¶
Revenons à la suite $T(n)$. Aussi étrange que cela puisse paraître à des débutants, la méthode la plus utilisée consiste à deviner la solution !
Ici, ce n'est pas très difficile. Si on ajoute 1 à $T(n)$, tout informaticien reconnaitra la suite $$1,2,4,8,16,32,64,128,256,1024,2048 ...$$ Il semble donc bien que $T(n)=2^n-1$. Mais on ne l'a pas démontré. C'est une conjecture.
C'est ici qu'intervient le raisonnement par récurrence : on vérifie que notre hypothèse $P(n):\ T(n)=2^n-1$ est vraie pour les premières valeurs de $n$ (ici $n=0$ suffit car $T(n)$ ne dépend que de $T(n-1)$), puis on montre que si $P(n-1)$ est vraie pour un certain $n$, alors, $P(n)$ est encore vraie.
On a bien $T(0)=0=2^0-1$. Si maintenant $T(n-1)=2^{n-1}-1$ pour un certain $n$, notre formule de récurrence donne $$T(n)=2T(n-1)+1=2(2^{n-1}-1)+1=2^n-2+1=2^n-1$$ CQFD.
Évidemment, la solution n'est pas toujours aussi facile à deviner. Les spécialistes connaissent par coeur un certain nombre de suites très fréquentes (en particulier, l'apparition de 42 après 1,2,5,14 suscite en général une certaine excitation), mais la tâche est facilitée par une base de données en ligne, The Online Encyclopedia of Integer Sequences, qui contient les premiers termes de centaines de milliers de suites accompagnées d'une fiche aussi détaillée que possible, avec en particulier une formule explicite si on en connait une. La recherche sur $1,3,7,15,31...$ conduit à cette page, sur laquelle on pourra constater que cette suite très simple est plus intéressante qu'il n'y paraît.
# Au passage, on peut écrire le programme
def f(n,i,j): # transfère n disques de i vers j
if n==1: print ("%d-->%d" % (i,j), end=' ')
else:
k = 6//(i*j) # Comme 6 = 1*2*3, les tiges sont i,j, et 6/(i*j)
f(n-1,i,k) # n-1 disques de i à k
f(1,i,j) # le grand disque de i à j
f(n-1,k,j) # n-1 disques de k à j
f(3,1,3)
f(8,1,3)
Méthode 2 : séries génératrices¶
La méthode la plus puissante pour résoudre des récurrences sans avoir à deviner quoi que ce soit fait appel à la notion de série génératrice.
L'idée est de représenter une suite $(u_n)_{n\ge 0}$ par un expression du type $$U(x) = u_0+u_1x+u_2x^2+u_3x^3+\cdots = \sum_{n\ge 0}u_n x^n.$$
Une telle expression s'appelle une série (entière) formelle. C'est en quelque sorte un polynôme de degré infini. On dit que c'est la série génératrice de la suite $(u_n)$.
Séries formelles vs séries convergentes¶
On qualifie ces séres de formelles pour les différencier des séries entières convergentes, qui servent à calculer les valeurs numériques de fonctions. Par exemple, si $x$ est un nombre vérifiant $|x|<1$, la série (dite géométrique) $$\sum_{n\ge 0}x^n =1+x+x^2+x^3+\cdots $$ converge vers $\frac1{1-x}$, ce que l'on démontre en remarquant que $$(1+x+x^2+x^3+\cdots+x^n)(1-x)=1-x^{n+1}$$ et que $x^{n+1}\rightarrow 0$ pour $n\rightarrow\infty$.
Ce n'est évidemment pas la meilleure méthode pour calculer $\frac1{1-x}$, mais si on intègre terme à terme cette identité (on peut prouver que c'est possible), on trouve $$\int_0^x\frac{1}{1-t}dt = \sum_{n\ge 0}\int_0^x t^ndt $$ c'est à dire $$\ln\left(\frac1{1-x}\right) = x+\frac12x^2+\frac13x^3+\frac14x^4\cdots$$ ce qui fournit un moyen de calculer les logarithmes. Par exemple, avec $x=\frac12$, la série converge et donne $\ln 2$.
from math import log # c'est ln en python
log(2) # valeur "exacte"
sum((0.5)**n/n for n in range(1,20)) # 19 termes de la série
sum((0.5)**n/n for n in range(1,50)) # 49 termes, on ne peut pas faire mieux à cause des erreurs d'arrondi
La plupart des fonctions usuelles ($\exp,\sin,\cos,\cdots$) admettent des développements de ce type. Il ne faut pas les confondre avec les développements limités, qui, comme leur nom l'indique, sont limités, et ne peuvent servir qu'à calculer des limites.
Dans le cadre des séries formelles, on s'interdit de donner des valeurs à la variable $x$. On se contente d'effectuer sur les séries les opérations usuelles (addition, multiplication, etc.). Les règles sont les mêmes que pour les polynômes (qui représentent les suites finies).
L'addition des séries correspond à l'addition des suites : $$A(x)=\sum_{n\ge 0}a_nx^n,\ B(x)=\sum_{n\ge 0}b_nx^n\quad \longrightarrow\quad A(x)+B(x)=\sum_{n\ge 0}(a_n+b_n)x^n.$$
La multiplication des séries est plus intéressante. Elle correspond à une opération appelée convolution sur les suites : $$A(x)B(x)= a_0b_0+(a_0b_1+a_1b_0)x+(a_0b_2+a_1b_1+a_2b_0)x^2+\cdots = \sum_{n\ge 0}\left(\sum_{i+j=n}a_ib_j\right)x^n$$ La suite $c=a*b$ donnée par $c_n=a_0b_n+a_1b_{n-1}+\cdots a_nb_0$ est appellée convolution des suites $a$ et $b$. Sur les séries, on voit immédiatement que cette opération est associative et commutative (puisque c'est le cas du produit des séries). La convolution est une opération fondamentale en traitement du signal et en automatique. On verra qu'elle intervient fréquemment dans les résolutions de récurrences.
Illustration de la méthode sur le cas des tours de Hanoi¶
Formons la série génératrice de la suite $u_n=T(n)$ :
$$U(x)= u_0 +u_1x + u_2x^2+u_3x^3+\cdots =u_0+\sum_{n\ge 1}u_nx^n.$$On sait que $u_0=0$, et que pour $n\ge 1$, $u_n=2u_{n-1}+1$. On remplace donc $u_0$ et $u_n$ par ces expressions, ce qui donne $$U(x)=0+\sum_{n\ge 1}(2u_{n-1}+1)x^n.$$ On va ensuite bricoler un peu le membre droit pour essayer de faire réapparaître $U(x)$ : $$U(x) = 0 + 2\sum_{n\ge 1}u_{n-1}x^n + \sum_{n\ge 1}x^n.$$ En écrivant $x^n=x\cdot x^{n-1}$, ça devient $$U(x) = 2x\sum_{n\ge 1}u_{n-1}x^{n-1} + x\sum_{n\ge 1}x^{n-1}.$$ Puisque dans ces sommes, $n$ commence à 1, $n-1$ commence à 0, et en posant $m=n-1$, on a finalement $$U(x)=2x\sum_{m\ge 0}u_mx^m+x\sum_{m\ge 0}x^m,$$ c'est à dire $$U(x)=2xU(x)+\frac{x}{1-x}.$$ Donc, $$(1-2x)U(x)=\frac{x}{1-x}$$ et finalement $$U(x)=\frac{x}{(1-2x)(1-x)}.$$ En quoi cette expression nous donne-t-elle la valeur de $u_n$ ? C'est une fraction rationnelle, dont on peut calculer une décomposition en éléments simples, et il est facile de développer les éléments simples en série entière.
Ici, le calcul est facile à faire à la main, mais pour les cas plus coriaces, on fera appel a sympy.
from sympy import * # C'est un module Python
var('x') # déclaration d'une variable formelle
U = x/((1-2*x)*(1-x))
U
apart(U) # La décomposition se fait avec la fonction "apart"
U.apart() # qui existe aussi comme méthode
Le programme nous a donc trouvé la décomposition (attention aux signes) $$U(x)= \frac1{1-2x}-\frac1{1-x}$$ (on écrit les dénominateurs sous la forme $1-X$ pour pouvoir utiliser la série géométrique), et on en déduit donc $$U(x)=\sum_{n\ge 0}(2x)^n-\sum_{n\ge 0}x^n= \sum_{n\ge 0}(2^{n}-1)x^n,$$ soit $u_n=2^n-1$.
Pour faire la calcul à la main, dans le cas où $$U(x)=\frac{A(x)}{(1-\beta_1x)(1-\beta_2x)\cdots(1-\beta_n x)}$$ avec
- $A(x)$ un polynôme de degré strictement inférieur à $n$
- les $\beta_i$ sont tous différents,
le calcul est très facile. On sait qu'il existe une décomposition de la forme $$U(x) = \frac{a_1}{1-\beta_1 x}+\frac{a_2}{1-\beta_2 x}+\cdots +\frac{a_n}{1-\beta_n x}$$ Pour trouver $a_i$, on multiplie cette égalité par $1-\beta_ix$. Alors, $$U(x)(1-\beta_ix) = a_i + \text{un truc qui s'annule pour $x=\frac1{\beta_i}$}.$$ Donc, $$a_i = U(x)(1-\beta_ix)|_{x=1/\beta_i}.$$
Sur notre exemple, $$U(x)= \frac{a_1}{1-2x}+\frac{a_2}{1-x}$$ avec $$a_1 = \frac{x}{1-x}|_{x=1/2}=1$$ $$a_2 = \frac{x}{1-2x}|_{x=1}=-1.$$
La suite de Fibonacci¶
Une autre suite célèbre qui peut être traitée par cette méthode est la suite de Fibonacci $$0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,\ldots$$ définie par la récurrence $$u_0=0,\ u_1=1,\quad u_n=u_{n-1}+u_{n-2}\ \text{pour $n\ge 2$}.$$ La série génératrice est $$U(x)=\sum_{n\ge 0}u_nx^n = u_0+u_1x+\sum_{n\ge 2}(u_{n-1}+u_{n-2})x^n= 0+x+ x\sum_{n\ge 1}u_{n-1}x^{n-1} +x^2\sum_{n\ge 2}u_{n-2}x^{n-2}$$ $$=x+x(U(x)-u_0)+x^2U(x) = x+xU(x)+x^2U(x) \quad\text{(puisque $u_0=0$)}$$ Donc $$(1-x-x^2)U(x)=x,\ \text{et finalement,}\ U(x)=\frac{x}{1-x-x^2}.$$ Pour continuer, il faut factoriser le dénominateur. On résout l'équation du second degré $$x^2+x-1 = 0$$ Le discriminant est $\Delta=(-1)^2-4(-1)=5$, les racines sont donc $$\alpha = \frac{-1+\sqrt{5}}{2}\ \text{et}\ \beta = \frac{-1-\sqrt{5}}{2}.$$ Pour ne pas traîner ces expressions dans la suite du calcul, on peut remarquer que comme $$(x-\alpha)(x-\beta)=x^2-(\alpha+\beta)+\alpha\beta=x^2+x-1,$$ on a $$\alpha+\beta=-1,\quad \alpha\beta = -1.$$ Alors, $$1-x-x^2 = -(\alpha-x)(\beta-x) = -\alpha\beta\left(1-\frac{x}{\alpha}\right)\left(1-\frac{x}{\beta}\right) =(1+\beta x)(1+\alpha x)$$ et en introduisant le nombre d'or $$\phi=\frac{1+\sqrt{5}}{2},\ \text{de sorte que}\ \beta=-\phi,\ \alpha=\frac1\phi,$$ on a finalement $$1-x-x^2 = \left(1-\phi x\right)\left(1+\frac{x}{\phi}\right).$$ On peut mainenant calculer la décomposition $$U(x) = \frac{a}{1-\phi x}+\frac{b}{1+\frac{x}{\phi}}$$ par la méthode précédente : $$a =\left. \frac{x}{1+\frac{x}{\phi}}\right|_{x=\frac1\phi} =\frac{1}{-\beta+\alpha}=\frac1{\sqrt{5}}$$ $$b = \left. \frac{x}{1-\phi}\right|_{x=-\phi}= \frac{-1}{\alpha+\beta}=-\frac1{\sqrt{5}}.$$ On obtient finalement la formule de Binet $$U(x) = \frac1{\sqrt{5}}\left[\frac1{1-\phi x}-\frac1{x+\frac{x}\phi}\right] = \frac1{\sqrt{5}}\sum_{n\ge 0}\left(\phi^n-(-1)^n\phi^{-n}\right)x^n$$ $$u_n=\frac1{\sqrt{5}}(\phi^n-(-\phi)^{-n}).$$
phi = (1+sqrt(5))/2
[float((phi**n-(-phi)**(-n))/sqrt(5)) for n in range(10)]
Exercice : La suite de Lucas¶
Elle est définie par la même récurrence que Fibonacci, $v_n=v_{n-1}+v_{n-2}$ , mais avec les conditions initiales $v_0=2$ et $v_1=1$. Alors (faire le calcul !), $$V(x) = 2+x+x(V(x)-2)+x^2V(x)$$ de sorte que $$V(x)= \frac{2-x}{1-x-x^2}.$$ Calculer la décomposition en éléments simples, et vérifier que $$v_n =\phi^n+(-\phi)^{-n}.$$
Attention, ici $v_0\not=0$ ...
[float(phi**n+(-phi)**(-n)) for n in range(10)]
Le monde de l'analyse et le monde des séries formelles¶
Résumons en quelques lignes le cours d'analyse de terminale scientifique. On y apprend que la dérivée de $x^n$ est $nx^{n-1}$ (pour $n\in\mathbb{Z})$; de sorte que $x^n$ est la dérivée de $\frac{x^{n+1}}{n+1}$, sauf pour $n=-1$. Pourtant, $\frac1x$ a bien une primitive, mais elle ne figure pas parmi les fonctions connues. On appelle logarithme naturel (ou néperien) $f(x)=\ln(x)=\int_1^x\frac{dt}t$ celle qui s'annule en 1. On remarque alors que $$\ln(ab)=\int_1^{ab}\frac{dt}t =\int_1^a\frac{dt}t+\int_a^{ab}\frac{dt}t=\ln a + \int_1^b \frac{du}u=\ln a+\ln b$$ en posant $u=at$.
On peut facilement étudier cette fonction, puisqu'on connaît sa dérivée. Elle est strictement croissante sur $]0,+\infty[$ et va de $-\infty$ à $+\infty$. Elle admet donc une fonction réciproque définie sur $]-\infty,+\infty[$ et à valeurs dans $]0,+\infty[$. On la note $\exp(x)$.
Comme $\ln(\exp(x)\exp(y))=\ln\exp(x)+\ln\exp(y)=x+y$, on a $$\exp(x)\exp(y)=\exp(x+y),$$ ce qui permet d'écrire $\exp(x)=e^x$ où $e=\exp(1)$ : c'est vrai pour $x$ rationnel, et pour $x$ quelconque, c'est à prendre comme une définition de la "puissance $x$".
Comment calculer ses valeurs ? Inspirés par l'exemple de la série du logarithme, on peut se demander s'il n'existerait pas une expression de la forme $$\exp(x)=a_0+a_1x+a_2x^2+\cdots =\sum_{n\ge 0}a_nx^n.$$ On a alors forcément $a_0=\exp(0)=1$. On peut trouver les suivants en remarquant que $a_1$ est la valeur en 0 de la dérivée $$0+a_1+2a_2x+3a_3x^2+\cdots$$ et d'une manière générale, la valeur en 0 de la dérivée $n$ième est $n!a_n$. Encore faut-il être capable de la calculer, mais $\exp(x)$ a le bon goût d'être sa propre dérivée. On aurait donc $n!a_n=1$ pour tout $n$. Ce n'est pas encore une démonstration, mais on a deviné le résultat correct et en travaillant un peu, on peut prouver que $$\exp(x)=\sum_{n\ge 0}\frac{x^n}{n!}$$ et ceci pour tout $x$.
Oublions maintenant tout ce qui précède, et intéressons nous à la série génératrice de la suite $u_n=\frac1{n!}$. Pour ne pas confondre les deux mondes, notons la $E(x)$: $$E(x)= \sum_{n\ge 0}\frac{x^n}{n!},$$ et calculons $$E(x)E(y)=\sum_{p\ge 0}\frac{x^p}{p!}\sum_{q\ge 0}\frac{y^q}{q!}= \sum_{p\ge 0}\sum_{q\ge 0}\frac{x^py^q}{p!q!}$$ Si on somme par diagonales $p+q=$constante, on obtient $$E(x)E(y)=\sum_{n\ge 0}\sum_{p+q=n}\frac{x^py^q}{p!q!}=\sum_{n\ge 0}\frac1{n!}\sum_{p+q=n}\frac{n!}{p!q!}x^py^q = \sum_{n\ge 0}\frac1{n!}\sum_{p=0}^n{n\choose p}x^py^{n-p}=\sum_{n\ge 0}\frac1{n!}(x+y)^n=E(x+y).$$ La formule $E(x)E(y)=E(x+y)$ est donc vraie aussi dans le monde des séries formelles, mais la démonstration dans ce cadre n'a rien à voir avec la version analytique. Dans le monde formel, cette identité est équivalente à la formule du binôme ! Alors que la propriété correspondante de la fonction exponentielle s'obtient par un changement de variable dans l'intégrale qui définit le logarithme.
Dans le cas ou une série formelle est le développement d'une vraie fonction (c'est à dire, si elle converge pour d'autres valeurs que $x=0$), on peut montrer que les formules vérifiées par la fonction sont aussi vérifées par la série, mais ça n'a rien d'évident. Remarquons aussi qu'il existe des séries formelles qui ne définissent aucune fonction, par exemple la série génératrice de la suite $n!$.