MPI 4 - Cours 2¶

Un peu de calcul non commutatif : séries rationnelles et langages rationnels¶

Considérons l'alphabet $A=\{a,b\}$, et intéressons nous au langage $L=(a+ba)^*$.

L'ensemble $C=\{a,ba\}$ est ce qu'on appelle un code préfixe, c'est à dire que s'il contient un mot $w$, il ne contient aucun préfixe $u$ de $w$ (un mot tel que $w=uv$ avec $u,v\not=\epsilon$). C'est un code, car tout mot de $C^*$ n'a qu'une seule écriture comme concaténation d'éléments de $C$ (unicité du déchiffrage, ou encore, non-ambiguïté de la grammaire) : $$w=baaabaaababaaa \rightarrow ba.a.a.ba.a.a.ba.ba.a.a$$ Le langage $L$ est reconnu par l'automate 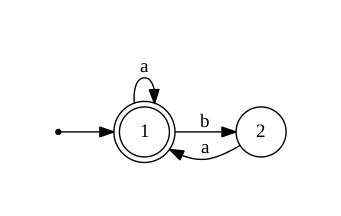Soit $u_n$ le nombre de mots de longueur $n$ dans $L$. On a $$L = \{\epsilon, a, ba, aa, baa, aba, aaa, baba,baaa,abaa,aaba,aaaa,\cdots\}$$ et donc $$u_0=1,\ u_1=1,\ u_2=2,\ u_3=3,\ u_4=5,\cdots$$ Si on note $L_n$ l'ensemble des mots de longueur $n$ dans $L$, on voit que pour $n\ge 2$, $$L_n=aL_{n-1}+baL_{n-2}$$ puisqu'un mot de $L$ commence soit par $a$, soit par $ba$. Donc, $u_n=u_{n-1}+u_{n-2}$ avec $u_0=1$, $u_1=1$, c'est donc la suite de Fibonacci décalée de 1.

Une technique classique pour étudier ce genre de problème est d'identifier les mots à des monômes en variables non commutatives, la concaténation devenant alors la multiplication et son élément neutre $\epsilon$ le scalaire 1. Le code $C$ s'identifie alores au polynôme $$C= a+ba$$ et le langage $L$ s'identifie à la série formelle $$L = C^* =\sum_{n\ge 0}C^n = 1+C+C^2+\cdots = \frac1{1-C}=\frac1{1-a-ba}=1+a+ba+baa+aba+aaa+\cdots.$$ On trouve alors automatiquement la série génératrice de $u_n$ en remplaçant $a$ et $b$ par $x$ dans cette expression, car les mots de longueur $n$ deviennent tous $x^n$ $$U(x)=\frac1{1-x-x^2}=1+x+2x^2+3x^3+5x^4+8x^3+\cdots$$ C'est donc la suite de Fibonacci décalée $u_n=F_{n+1}.$

D'une manière générale, l'expression $C^*$ se traduit par $(1-C)^{-1}$, mais on ne peut en déduire le dénombrement des mots par longueur que si l'expression est non ambiguë. Par exemple, $C=a+ab+ba$ n'est pas un code, puisque $w=aba$ possède deux dérivations : $w=a.ba = ab.a$. Dans la série non commutative $$(1-a-ab-ba)^{-1}=1+a+ab+ba+ 2aba+aab+baa+aaa+\cdots$$ le coefficient d'un mot est le nombre de ses factorisations en éléments de $C$. On peut montrer en construisant l'automate minimal de $C^*$ qu'une expression non ambigue serait $$((b+a(a+ba)^*bb)a)^*(\epsilon+a((a+ba)^*(\epsilon+b))$$ En remplaçant $a$ et $b$ par $x$ et les $X^*$ par des $(1-X)^{-1}$, on trouve pour la série génératrice $$ \frac1{1-x-2\,{x}^{2}+{x}^{3}}=1+x+3\,{x}^{2}+4\,{x}^{3}+9\,{x}^{4}+14\,{x}^{5}+28\,{x}^{6}+47\,{x}^{7}+89\,{x}^{8}+155\,{x}^{9}+286\,{x}^{10}+507\,{x}^{11}+O \left( {x}^{12} \right)$$ Si on avait fait cela avec l'expression ambiguë, on aurait trouvé le résultat faux $$\frac1{1-x-2x^2}=1+x+3\,{x}^{2}+5\,{x}^{3}+11\,{x}^{4}+21\,{x}^{5}+43\,{x}^{6}+85\,{x}^{7}+171\,{x}^{8}+341\,{x}^{9}+683\,{x}^{10}+1365\,{x}^{11}+O \left( {x}^{12} \right)$$

La décomposition en éléments simples¶

Lorsque la série génératrice d'une suite représente une fraction rationnelle, on peut la décomposer en éléments simples, pourvu que l'on connaisse les racines du dénominateur : si $$U(x) = \frac{A(x)}{B(x)}$$ avec $$B(x)=(x-\beta_1)^{m_1}(x-\beta_2)^{m_2}\cdots(x-\beta_n)^{m_n}$$ alors, on peut trouver une décomposition de la forme $$U(x)=P(x) +\sum_{k=1}^n\sum_{i_k=1}^{m_k}\frac{a_{ik}}{(x-\beta_k)^{i_k}}$$ où $P(x)$ est un polynôme (qui n'apparaît que si le degré de $A$ est supérieur ou égal à celui de $B$, auquel cas c'est le quotient de $A$ par $B$), et pour chaque racine $\beta$, on a un élément simple $\frac1{(x-\beta)^k}$ pour $k$ de 1 jusqu'à la multiplicité $m$ de $\beta$.

from sympy import *
init_printing()
var('x')

# Exemple au hasard
U = (2*x**12-x**3+x+2)/((1-2*x)**3*(1+3*x)**2*(1-x)**4);U

U.apart()

Notons que cette décomposition peut faire intervenir des racines complexes ou irrationnelles. Pour que sympy accepte de les calculer (s'il ne doit résoudre que des équations de degré au plus 4), il faut utiliser l'option full=True et la méthode doit.

V = 1/(1+x+x**2);V

V.apart()

V.apart(full=True).doit()

# Avec des équations du 3ème degré, le résultat n'est pas très exploitable ...
www=1/(1+x+x**3)
www.apart(full=True).doit()

La formule du binôme généralisé¶

On voit qu'il faut être capable de développer en série entière les fractions simples $$\frac1{(1-x)^k}.$$ Pour $k=1$, c'est fait. On peut traiter $k=2$ en l'élevant au carré. En utilisant la formule générale de produit $$\sum_{p\ge 0}a_px^p\sum_{q\ge 0}b_qx^q = \sum_{n\ge 0}\left(\sum_{p=0}^na_pb_{n-p}\right)x^n$$ on a $$\left(\frac1{1-x}\right)^2 = \sum_{n\ge 0}\left(\sum_{p=0}^n 1\times 1\right)x^n=\sum_{n\ge 0}(n+1)x^n$$ Pour peu que l'on sache que $$1+2+\cdots +n = \frac{n(n+1)}{2}$$ on peut remultiplier par $\frac1{1-x}$ et obtenir $$\left(\frac1{1-x}\right)^3 = \sum_{n\ge 0}\left(\sum_{p=0}^n (p+1)\times 1\right)x^n=\sum_{n\ge 0}\frac{(n+1)(n+2)}2x^n$$ Avec un effort supplémentaire, on peut encore trouver $k=4$ et deviner la formule générale $$\left(\frac1{1-x}\right)^k = \sum_{n\ge 0}{n+k-1\choose n}x^n$$ et la prouver par récurrence.

Ou encore, la prouver combinatoirement : si on fait le produit de $k$ séries géométriques $$\frac1{(1-x_1)(1-x_2)\cdots (1-x_k)}=\sum_{n_1\ge 0}x_1^{n_1}\sum_{n_2\ge 0}x_2^{n_2}\cdots\sum_{n_k\ge 0}x_k^{n_k},$$ on voit que le membre droit est la somme de tous les monômes en $x_1,\ldots,x_k$. Si l'on pose $$x_1=x_2=\cdots=x_k=x$$ dans cette égalité, le membre gauche devient $\left(\frac1{1-x}\right)^k$, et le coefficient de $x^n$ dans le membre droit est le nombre de monômes de degré total $n$ que l'on peut former avec $k$ variables, c'est à dire, le nombre de sélections avec répétitions de $n$ objets parmi $k$, connu pour être égal à ${n+k-1\choose n}x^n$ d'après le cours de L2.

series(1/(1-x)**2,x,0,10)

series(1/(1-x)**3,x,0,10)

series(1/(1-x)**4,x,0,10)

On peut faire encore mieux. Rappelons qu'on définit $x^{p/q}$ comme $\sqrt[q]{x^p}$, et qu'on peut définir $x^\alpha$ pour $\alpha$ réel quelconque comme $\exp(\alpha\ln x)$.

On peut donc donner un sens à la série formelle $(1+x)^\alpha$ pour $\alpha$ quelconque. Posons $$(1+x)^\alpha = \sum_{n\ge 0}a_nx^n$$ et cherchons les coefficients $a_n$.

On définit la dérivation des séries formelles en posant $(x^n)'=\frac{d}{dx}x^n=nx^{n-1}$ et en prolongeant par linéarité. Il n'est pas difficile de monter que cette opération vérifie les propriétés usuelles de la dérivée des fonctions. Par exemple, pour montrer $(fg)'=f'g+fg'$, on commence par le vérifier pour $f=x^p$ et $g=x^q$. Puis on utilise un première fois la linéarité pour en déduire que c'est encore vrai pour $f=x^p$ et $g$ quelconque, puis une seconde fois pour $f$ et $g$ quelconques.

On en déduit ensuite par récurrence $(f^n)'=nf^{n-1}f'$, puis par linéarité, $g(f(x))'=g'(f(x))f'(x)$.

Comme $(1+x)^\alpha = \exp(\alpha\ln(1+x))$, on a $$\frac{d}{dx}(1+x)^\alpha = \exp(\alpha\ln(1+x))\alpha\frac1{1+x}=\alpha(1+x)^{\alpha-1},$$ comme on pouvait s'y attendre.

On peut maintenant écrire $$(1+x)\frac{d}{dx}(1+x)^\alpha = (1+x)\sum_{n\ge 0}n a_nx^{n-1}=\alpha (1+x)^\alpha=\sum_{n\ge 0}\alpha a_nx^n.$$ En effectuant le produit par $1+x$, on trouve $$\sum_{n\ge 0}(n+1)a_{n+1}x^n+\sum_{n\ge 0}na_nx^n=\sum_{n\ge 0}\alpha a_nx^n$$ donc, en identifiant les coefficients de $x^n$ $$(n+1)a_{n+1}=(\alpha-n)a_n,\ \text{d'où}\ a_{n+1}=\frac{\alpha-n}{n+1} \frac{\alpha-n+1}{n} \frac{\alpha-n+2}{n-1}\cdots \frac{\alpha}{1}a_0. $$ Comme on a clairement $a_0=1$, on a finalement $$a_n = \frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!} =: {\alpha\choose n}.$$ Ces nombres sont appeliés coefficients binomiaux généralisés. Quand $\alpha$ est un entier positif, ils coincident évidemment avec les coefficients binomiaux ordinaires.

Exemple : $\alpha=\frac12$¶

On a $\def\a{\frac12}$ $${1/2\choose n}=\frac{\a(\a-1)(\a-2)\cdots(\a-n+1)}{n!} =\frac{1(1-2)(1-4)\cdots(1-2n+2)}{2^nn!} =(-1)^{n-1}\frac{1\cdot 3\cdot 5\cdots (2n-3)}{2^nn!}$$ $$= (-1)^{n-1}\frac{(2n-2)!}{2^{n-1}(n-1)!2^nn!}= \frac{(-1)^{n-1}}{2^{2n-1}}\frac1{n}{2n-2\choose n-1}.$$

Application : dénombrement des arbres binaires¶

Un arbre binaire complet, c'est soit un sommet unique o, soit

    o
   / \
  A   B

où A et B sont des arbres binaires complets. Soit $c_n$ le nombre d'arbre binaires complets à $n$ feuilles. Les premiers exemples sont

o         o                             o            o
         / \                           / \          / \
        o   o                         o   o        o   o
                                     / \              / \
                                    o   o            o   o


    _o__           __o___           __o__           __o___           _o__    
   /    \         /      \         /     \         /      \         /    \   
  o     _o_      o       _o_      o       o      _o_       o      _o_     o  
       /   \            /   \    / \     / \    /   \            /   \       
      o     o          o     o  o   o   o   o  o     o          o     o      
           / \        / \                           / \        / \           
          o   o      o   o                         o   o      o   o

On a donc $c_0=0$, $c_1=1$, $c_2=1$, $c_3=2$, $c_4=5$.

Comment calculer les $c_n$ ?

Un arbre à $n$ feuilles aura un sous-arbre gauche $A$ à $p$ feuilles et un sous-arbre droit $B$ à $q$ feuilles, avec $p+q=n$. Il y a $c_pc_q$ choix pour ces sous-arbres, et $p,q$ sont au moins égaux à 1 et au plus à $n-1$. Donc, pour $n\ge 2$, $$c_n = \sum_{p=1}^{n-1}c_pc_{n-p} =c_1c_{n-1}+c_2c_{n-2}+\cdots+c_{n-1}c_1.$$ C'est une récurrence qui fait intervenir toutes les valeurs précédentes. Testons là : $$c_2 = c_1c_1 = 1,$$ $$c_3=c_1c_2+c_2c_1=1+1=2,$$ $$c_4=c_1c_3+c_2c_2+c_3c_1=2+1+2=5,$$ $$c_5=c_1c_4+c_2c_3+c_3c_2+c_4c_1=5+2+2+5=14,$$ $$c_6=c_1c_5+c_2c_4+c_3c_3+c_4c_2+c_5c_1=14+5+4+5+14=42, \ldots$$ Ces nombres sont très célèbres. On les appelle nombres de Catalan, bien qu'ils aient été découverts par Euler qui les appelait lui-même nombres de Segner. Ce livre de Richard Stanley en recense 214 interprétations différentes.

Formons la série génératrice $$C(x)=\sum_{n\ge 0}c_n x^n = 0 +x+x^2+2x^3+5x^4+14x^5+42x^6+\cdots$$ Puisque $c_0=0$, la récurrence s'écrit aussi bien $$c_n = \sum_{p=0}^{n}c_pc_{n-p} \quad\text{pour $n\ge 2$} $$ Le membre droit est le coefficient de $x^n$ dans $C(x)^2$. Comme $C(x)$ commence par $x$, $C(x)^2$ commence par $x^2$, et on a donc en complétant $$C(x) = x + C(x)^2.$$ Autrement dit, $C(x)$ est solution de l'équation du second degré $$X^2-X+x=0,$$ de discriminant $1-4x$, de sorte que $$C(x)=\frac{1\pm\sqrt{1-4x}}{2}$$ On sait que $\sqrt{1-4x}=1-\frac12 x+O(x^2)$ par la formule du binôme généralisé, il faut donc choisir la solution avec le signe moins si l'on veut que son premier terme soit $x$ $$C(x)=\frac{1-\sqrt{1-4x}}{2}= \frac12\left[1-\sum_{n\ge 0}{1/2\choose n}(-4x)^n\right] =\sum_{n\ge 1}\frac{(-1)^{n}}{2^{2n}}\frac1{n}{2n-2\choose n-1}(-4x)^n =\sum_{n\ge 1}\frac1{n}{2n-2\choose n-1}x^n$$ ce qui nous donne finalement $$c_n = \frac1{n}{2n-2\choose n-1}.$$ Vérifions : $$c_6 = \frac16{10\choose 5}=\frac16 252 = 42.$$

[binomial(2*n-2,n-1)//n for n in range(1,12)]