:: Enseignements :: ESIPE :: E4INFO :: 2013-2014 :: Algorithmique avancée ::

Recherche du plus court chemin dans un champ d'obstacles

EXTENSION DE LA DATE LIMITE:
Dimanche 8 décembre 23h59

Introduction

Le but du projet est de trouver le chemin le plus court entre deux points dans un champ d'obstacles. Le champ est un tableau à deux dimensions. Chaque case du tableau indique si elle est disponible ou s'il y a un obstacle à cet endroit. L'objectif est de trouver la séquence la plus courte de déplacements élémentaires afin de se déplacer d'une case à une autre en évitant les obstacles. Il y a huit déplacements élémentaires: déplacements d'une case verticalement vers la droite et vers la gauche, déplacements d'une case horizontalement vers la droite et vers la gauche, déplacements en diagonale d'une case en haut à gauche, en haut à droite, en bas à gauche et en bas à droite.

L'idée du projet est de représenter le champ d'obstacles sous la forme d'un graphe. Chaque case correspond à un sommet. Il existe un arc entre deux sommets s'il existe un déplacement élémentaire permettant de se déplacer entre les deux cases correspondantes. Un déplacement élémentaire à partir ou à destination d'une case d'un obstacle est interdit. Dans un premier temps, toutes les arêtes du graphe auront un coût de 1.

Entrées-sorties

La première partie du projet consiste à gérer les entrées et les sorties.

Entrée:

Le programme reçoit en entrée un fichier XML décrivant le champ d'obstacles (obstacles), ainsi que les points de départ (start) et d'arrivée (end) du plus court chemin à calculer. Ce fichier XML suit le format suivant:

<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<xml>
  <rectangle>
    <dimension height="10" width="10"/>
    <obstacles>
      <obstacle topleftx="2" toplefty="3" bottomrightx="4" bottomrighty="4" />
      <obstacle topleftx="4" toplefty="5" bottomrightx="5" bottomrighty="8" />
      <obstacle topleftx="7" toplefty="2" bottomrightx="7" bottomrighty="5" />
    </obstacles>
  </rectangle>
  <points>
    <start x="0" y="0"/>
    <end x="9" y="9"/>
   </points>
</xml>

Un obstacle est défini comme un rectangle par son point supérieur gauche (topleftx, toplefty) et son point inférieur droit (bottomrightx, bottomrighty).

Sortie:

Le programme génère un fichier image (PNG) correspondant au champ d'obstacles (cases vides en blanc, obstacles en noir) avec le plus court chemin marqué en bleu (s'il a été calculé). Les points de départ et d'arrivée seront marqués en rouge. La bordure doit être en noir. Le fichier XML ci-dessus donne l'image suivante (lorque le chemin le plus court n'est pas calculé):

Pour information: en java, vous pouvez facilement générer un fichier PNG à l'aide de la classe BufferedImage. Voici un exemple de code:

    BufferedImage bi = new BufferedImage(1000, 1000, BufferedImage.TYPE_INT_ARGB);
    for(int i = 250 ; i < 750 ; i++){
       for(int j = 250 ; j < 750 ; j++){
          bi.setRGB(i, j, Color.BLUE.getRGB());
       }
    }
    File outputfile = new File("saved.png");
    ImageIO.write(bi, "png", outputfile);

Jeu de tests:

Délivrable 1:
Ecrire un programme qui:

prend en entrée un fichier XML décrivant le champ d'obstacles
charge celui-ci dans un graphe (représenté par des listes d'adjacence)
génère le fichier PNG (sans afficher le chemin le plus court).

Le programme sera lancé avec la ligne de commande suivante:

  java ProjetAlgo -i input.xml -o output.png

où input.xml correspond au fichier XML de description du champ d'obstacles et output.png correspond à l'image PNG générée par le programme.

Recherche du plus court chemin par l'algorithme de Dijkstra

L'idée du projet est d'utiliser l'algorithme de Dijkstra en utilisant une file de priorité pour trouver le plus court chemin dans le champ d'obstacles (représenté par un graphe).

Délivrable 2:
Ecrire un programme qui:

implante l'algorithme de Dijkstra en utilisant une file de priorité
l'applique sur le graphe correspondant au champ d'obstacles décrit dans un fichier XML
génère le fichier PNG affichant le champ d'obstacles et le chemin le plus court pour aller du point de départ au point d'arrivée.

Pour la file de priorité, vous pourrez utiliser la classe PriorityQueue ou TreeSet. Il vous est demandé de prêter une attention particulière à la complexité des méthodes utilisées.

Le programme sera lancé avec la ligne de commande suivante:

  java ProjetAlgo --with-shortest-path -i input.xml -o output.png

où input.xml correspond au fichier XML de description du champ d'obstacles et output.png correspond à l'image PNG générée par le programme. L'option --with-shortest-path indique que le programme doit calculer le plus court chemin.

Optimisation

La méthode décrite ci-dessus est très couteuse en espace mémoire (pour de très gros champs d'obstacles). Nous souhaitons donc l'optimiser en réduisant le graphe sur lequel va être appliqué l'algorithme de Dijkstra.

Tout d'abord, il est possible de limiter l'ensemble de sommets du graphe aux points de début et de fin du chemin, ainsi qu'aux sommets correspondant aux cases dans les coins des obstacles.
Ensuite, il existe un arc entre deux sommets s1(x1,x2) et s2(x2,y2) si s1 est visible par s2 (i.e. il n'y a pas d'obstacle coupant la droite passant par s1 et s2).
Les arcs du graphe sont désormais pondérés par la fonction h définie telle que:

  h(s1,s2) = max(abs(x1 - x2),abs(y1-y2))

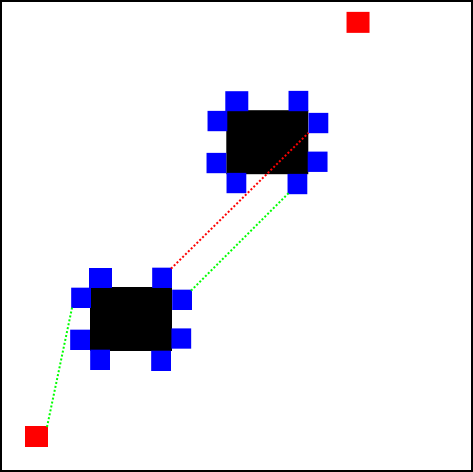
Dans la figure ci-dessous, les obstacles sont en noir et les points de départ et d'arrivée en rouge. Les cases en coin d'obstacles (à garder comme sommets) sont marqués en bleu. Le trait en pointillé rouge relie un exemple de couple de sommets non visibles l'un par rapport à l'autre. Chaque trait en pointillé vert relie un exemple de couple de sommets visibles l' un par rapport à l'autre.

La réduction du graphe peut se faire à l'aide l'algorithme suivant:

    for all sommets u
      for all sommets v
        if v est visible par u pour tous les obstacles
          ajouter une arete entre u et v de poids h(u,v)
        end if
      end for
    end for

    function visible(entiers ux, uy, vx, vy, ax, ay, bx, by)
        // ux, uy, vx, vy sont les coordonnees des sommets u et v
        // ax, ay, bx, by sont des coordonnees d'un obstacle
        // resultat : vrai si v est visible par u par rapport a l'obstacle

        test = 
        intersection(2*ux+1,2*uy+1,2*vx+1,2*vy+1,2*ax,2*ay,2*bx+2,2*by+2) ||
        intersection(2*ux+1,2*uy+1,2*vx+1,2*vy+1,2*ax,2*by+2,2*bx+2,2*ay)
          
        return !test
        
    end function
    
    function intersection(entiers ax, ay, bx, by, cx, cy, dx, dy)

        t1 = sign((cx-ax)*(by-ay) - (bx-ax)*(cy-ay))
        t2 = sign((dx-ax)*(by-ay) - (bx-ax)*(dy-ay))
        
	if (t1*t2 >= 0) then
	    return false
        end if
        
        t3 = sign((ax-cx)*(dy-cy) - (dx-cx)*(ay-cy))
        t4 = sign((bx-cx)*(dy-cy) - (dx-cx)*(by-cy))

        return (t3*t4 < 0)

    end function

Jeu de tests:

Délivrable 3:
Ecrire un programme qui fait la même chose que le délivrable 2, à l'exception que le graphe doit être réduit avant l'application de l'algorithme de Dijkstra.

Le programme sera lancé avec la ligne de commande suivante:

  java ProjetAlgo --with-shortest-path -r -i input.xml -o output.png

où input.xml correspond au fichier XML de description du champ d'obstacles et output.png correspond à l'image PNG générée par le programme. L'option -r indique le programme fait l'optimisation de réduction du graphe. L'option --with-shortest-path indique que le programme doit calculer le plus court chemin.

Rendu

Ce projet doit être réalisé en binomes, en Java. Il devra être envoyé avant le 8 décembre 2013, 23h59, à votre chargé de TP. Le message aura pour objet "[Algo IR2] Projet de NOM1 et NOM2". Il contiendra une archive .tgz, contenant les sources de votre code, les exécutables, les informations pour compiler votre code et un rapport (en pdf). Le rapport ne devra pas dépasser 4 pages. Dans ce rapport, vous décrirez, en particulier, les structures de données utilisées et vous discuterez des complexités en temps et en espace des algorithmes implantés. Si vous avez réalisé la partie "Optimisation", il conviendra d'expliquer pourquoi l'algorithme marche et de discuter les défauts et qualités de la procédure de réduction implantée.