:: Enseignements :: ESIPE :: E3INFO :: 2021-2022 :: Algorithmique ::
Le but de ce TP est de manipuler les arbres binaires. On implémente des parcours en profondeur et des fonctions récursives de base sur des arbres binaires. On implémente également des fonctions pour visualiser les arbres en utilisant l'outil dot.
![[LOGO]](http://igm.univ-mlv.fr/ens/resources/mlv.png) | Arbres binaires |
Le but de ce TP est de manipuler les arbres binaires. On implémente des parcours en profondeur et des fonctions récursives de base sur des arbres binaires. On implémente également des fonctions pour visualiser les arbres en utilisant l'outil dot.
Exercice 1 - Premier arbre
- Récupérer l'archive Base.zip et extraire les fichiers dans votre répertoire de travail. Les fichiers tree.h et tree.c contiennent les définitions de type pour représenter un arbre binaire d'entiers ainsi qu'une fonction pour allouer un noeud. Makefile permet de générer un exécutable de nom ./tp07.
-
Modifier la fonction main du fichier tp07.c pour
qu'elle crée l'arbre suivant, en utilisant la fonction create_node :
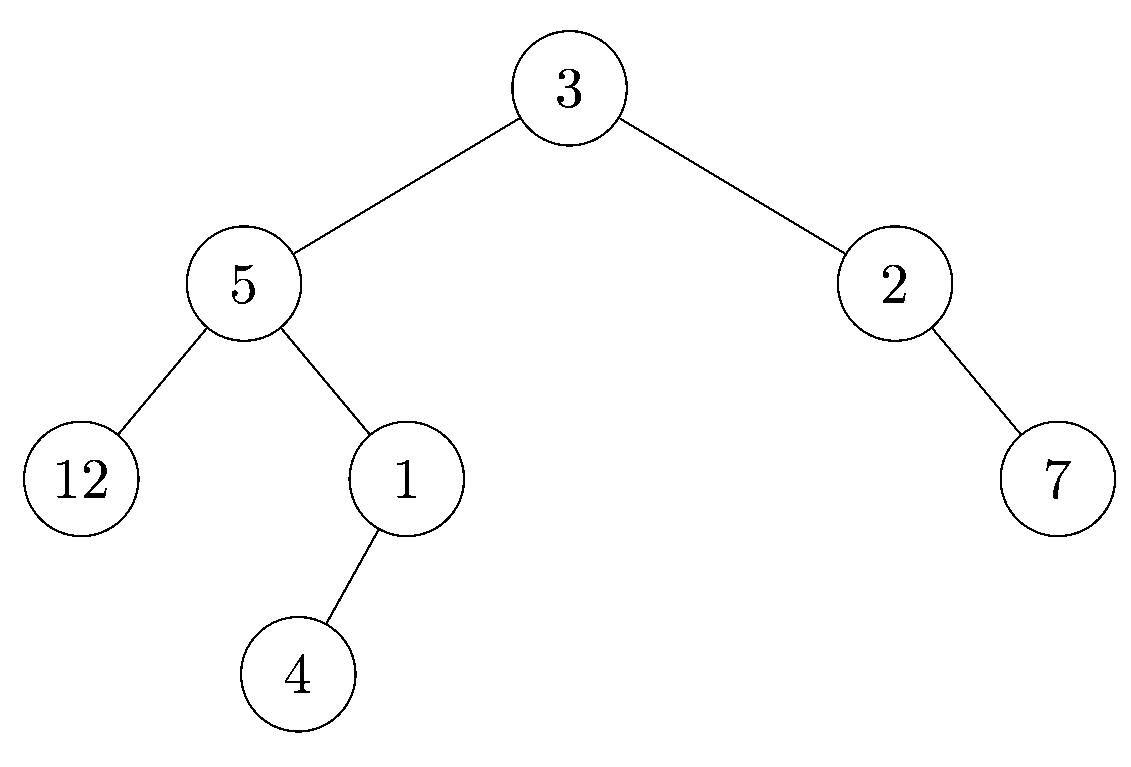
Exercice 2 - Parcours en profondeur
Ajouter à tree.h et à tree.c,
les prototypes et les définitions pour les fonctions suivantes :
- void display_prefix(node *t) qui affiche les valeurs des noeuds de l'arbre t en ordre préfixe ;
- void display_infix(node *t) qui affiche les valeurs des noeuds de l'arbre t en ordre infixe ;
- void display_suffix(node *t) qui affiche les valeurs des noeuds de l'arbre arb en ordre suffixe.
- Tester les fonctions sur l'arbre créé dans l'exercice précédent.
Exercice 3 - Visualisation
-
Copier le code suivant dans un fichier arbre.dot.
digraph tree { splines=false node [shape=record,height=.1] edge [tailclip=false, arrowtail=dot, dir=both]; n0 [label="<left> | <value> 5 | <right>"]; n0:left:c -> n1:value; n1 [label="<left> | <value> 7 | <right>"]; n0:right:c -> n2:value; n2 [label="<left> | <value> 3 | <right>"]; n2:right:c -> n3:value; n3 [label="<left> | <value> 1 | <right>"]; }Dans ce code, les identificateurs n0, n1, n2, n3 désignent les quatre noeuds de l'arbre de la figure ci-dessous. Sur la ligne 6, le noeud n0 qui contient l'entier 5 est déclaré. Puis, sur la ligne 7, on déclare que ce noeud a un fils gauche, le noeud n1: on relie n0:left:c avec n1:value. Cela dit au programme dot de dessiner une arête du centre de la partie left du noeud n0 vers la partie value du noeud n1.
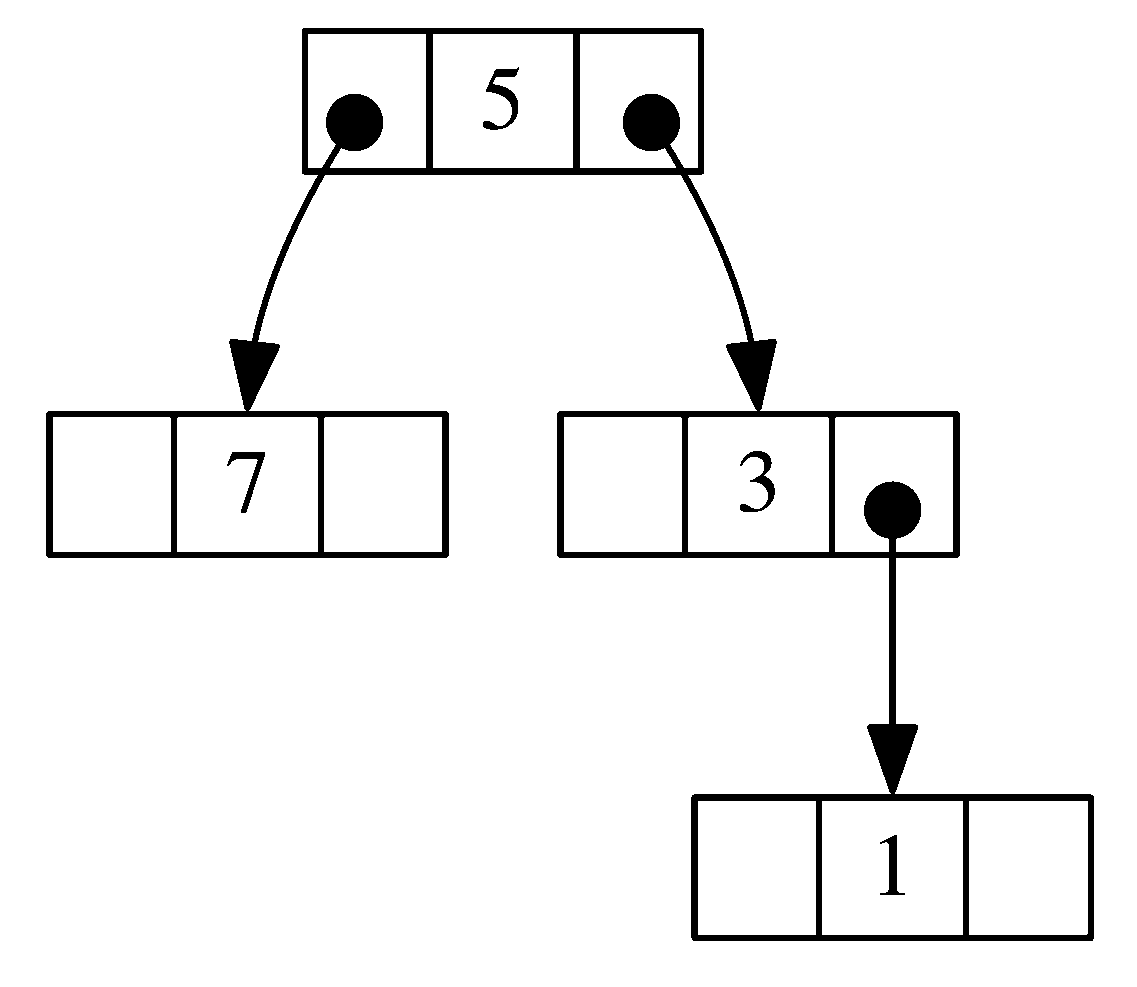
Vous trouverez la documentation du langage DOT sur le lien suivant : Taper dans un terminaldot -Tpdf arbre.dot > arbre.pdf evince arbre.pdf &>/dev/null &
pour construire le graphique et le visualiser.
Si vous utilisez un autre visualiseur que evince sur votre système, vous devez changer le nom evince au nom de votre visualiseur préféré et vous n'avez pas forcement besoin d'ajouter &>/dev/null.
Si vous avez besoin d'installer le programme dot, il fait partie du logiciel graphviz. -
Dans l'archive Base.zip se trouvent les fichiers
visualtree.h et visualtree.c.
Essayer la fonction main suivante, compiler et exécuter :
#include "tree.h" #include "visualtree.h" #include <stdio.h> int main() { node *t = NULL; write_tree(t); return 0; }La fonction write_tree dans visualtree.h/.c génère le fichier current-tree.pdf. Vous pouvez l'ouvrir dans le visualiseur evince en tapant evince current-tree.pdf &>/dev/null &. -
La fonction void write_tree_aux(node *t) (dans visualtree.c) ignore pour
l'instant l'argument t.
Elle construit simplement un arbre codé en dur, génère le code DOT correspondant
dans le fichier current-tree.dot et convertit ce fichier en pdf.
Modifier cette fonction pour qu'elle génère le code
DOT qui correspond à l'arbre t donné en argument.
Indice : Faire un parcours en profondeur de l'arbre. Pour chaque noeud visité, écrire la ligne (en code dot) pour déclarer le noeud et les lignes pour le relier à ses fils (s'ils existent). - Dans la suite, vous pouvez utiliser la fonction write_tree pour vérifier que vos arbres sont bien construits. Notez que si vous laissez evince ouvert (lancé en arrière-plan avec evince current-tree.pdf &>/dev/null &) alors le visualiseur affiche automatiquement les mises à jour du fichier current-tree.pdf. Donc, si votre programme fait plusieurs appels à la fonction write_tree, alors vous pouvez suivre les modifications de l'arbre dans le visualiseur.
Exercice 4 - Construction
Dans cet exercice, un arbre sera représenté par une suite d'entiers.
La suite correspond à un parcours en profondeur en ordre préfixe de l'arbre.
Un entier 0 représente le traitement d'un arbre vide (NULL).
Un entier x strictement positif représente le traitement d'un noeud contenant x.
Exemple : L'arbre de la figure de l'exercice 1 est représenté par la suite 3 5 12 0 0 1 4 0 0 0 2 0 7 0 0
Ajouter à tree.h et à tree.c, le prototype et la définition de la fonction node *scan_tree(void) qui construit un arbre binaire à partir d'une suite d'entiers lue au clavier. La fonction renvoie un pointeur sur la racine de l'arbre construit.
Le comportement de la fonction est le suivant :
Exemple : L'arbre de la figure de l'exercice 1 est représenté par la suite 3 5 12 0 0 1 4 0 0 0 2 0 7 0 0
Ajouter à tree.h et à tree.c, le prototype et la définition de la fonction node *scan_tree(void) qui construit un arbre binaire à partir d'une suite d'entiers lue au clavier. La fonction renvoie un pointeur sur la racine de l'arbre construit.
Le comportement de la fonction est le suivant :
- lire un entier x au clavier
- si x == 0, alors renvoie NULL
- sinon appeller récursivement scan_tree sur le fils gauche et le fils droit
- créer un noeud contenant l'entier x et rattacher les arbres représentant le fils gauche et le fils droit
Exercice 5 - Mesures
Ajouter à tree.h et à tree.c,
les prototypes et les définitions des fonctions suivantes :
- int count_nodes(node *t) qui renvoie le nombre de noeud de l'arbre t ;
- int count_leaves(node *t) qui renvoie le nombre de feuilles de l'arbre t ;
- int count_only_children(node *t) qui renvoie le nombre d'enfants uniques de l'arbre t. Un noeud est un enfant unique s'il est le seul enfant de son parent.
- int height(node *t) qui renvoie la hauteur de l'arbre t ;
Exercice 6 - Nettoyage
Ajouter à tree.h le prototype et la définition d'une fonction
récursive
void free_tree(node *t) qui libère toute
mémoire associée à l'arbre t.
© Université de Marne-la-Vallée